Notes on "obstacle avoidance" for the course
on Physically Based Modeling at SIGGRAPH 88,
August 1 through 5 in Atlanta, Georgia.
Craig W. Reynolds
[Updated Contact Information]
(The author thanks Christopher Kline <ckline@acm.org> for kindly converting this paper to html.)
This paper discusses some techniques for directing the paths of objects moving around an environment, normally towards specified goals, such that they do not collide with either static obstacles or other moving objects. Most of these techniques apply equally well to motion in three-dimensional space or on two-dimensional surfaces. The intended application is the control of motion of geometrical models in simulated environments, such as in the production of computer animation. Similarly, they are useful in certain types of simulation studies for engineering applications, such as modeling the flow of machines and people around each other on a factory floor. Some of the techniques are applicable to control of the motion of real physical objects such as robotic vehicles.
It is possible to pre-specify paths around a static environment. Indeed, this is by far the most common technique for describing motion for animation. A series of control points is specified which describe a splined curve in space. The object is moved along the curve at a scripted rate. For simple, well-defined motion this is probably the most convenient and direct technique for controlling the animation.
For complex environments (with hundreds or even thousands of objects) and so presumably for correspondingly complex paths, such pre-specification can become quite tedious. And in a situation where the environment is not static, where in fact all of the objects might be in motion themselves, it is simply not practical to try to fully specify all paths beforehand. In an environment where the obstacles are moving along unpredictable paths (perhaps as the result of a simulation process) the only way to reliably move an object while avoiding collisions is to abandon pre-specification and use an active navigation algorithm "while" the object is in motion. The object must be able to react to the current state of the dynamic environment and steer a path around moving obstacles. A recent example of this sort of motion control technique is a system for producing animated simulations of bird flocks and related types of coordinated group motion [8].
Underlying this type of motion control (steering objects around obstacles toward goals) is the concept of self-directed action. Rather than the traditional view of inert geometrical objects being moved according to a centralized, pre-existing plan (the script specified by the animator), here we consider the objects to be active independent entities capable of directing their own motion. They are not merely inert geometrical models but rather "self-motivated" behavioral models, which also happen to have a geometric component. They are, to use Ann Marion's apt phrase, "puppets that pull their own strings." Actually, most convenient are hybrid objects that can be directed in general terms from an animator's script but that can handle details of their own behavior as required. Specifically, the animator can set up goals for the behavioral objects, but the objects themselves will work out the specifics, such as the exact path that they take to avoid collisions with obstacles. Furthermore, the "guiding hand" of the animator is not required; behavioral objects are perfectly happy to merely wander around on their own, ad libbing their roles as "extras."
This sort of independent, self-directed behavioral agent is modeled by a construct called an actor [5, 2]. An actor is a combination of a process (perhaps a processor) and an object in the sense of an object oriented programming system, which is itself a combination of data structure and behaviors (programs).
The motion of these constructs is based on geometrical transformations on objects made in their own local coordinate space. They are a three-dimensional version of the turtle of the Logo programming language [1], and move according to the rules of turtle geometry. Each such object has position and orientation and maneuvers relative to that state: it moves "forward" along its own local Z axis, and turns right or left, up or down, relative to its current orientation. In addition to geometric state, the "flying turtles" described here also have dynamic state in the forrn of velocity and hence conserve momentum. The object's behavior alters its dynamic geometric state by the application of steering accelerations.
The type of motion discussed here is somewhat related to the idea of constraint- based motion (using "constraint maintenance" systems). One typical application of a constraint system would be to specify behavior in the event of a collision between objects. The "steering around obstacles" technique seeks to prevent collisions, and if steering accelerations are not bounded it will usually succeed. But in a more realistic, physically based model, the steering accelerations would be strictly limited, and so collisions become a possibility. One of the obstacle avoidance techniques discussed below is implemented in terms of the underlying constraint maintenance system.
Systems based on this model of distributed behavioral control [8] are often confused with artificial intelligence. This is understandable because there is some overlap, and because artificial intelligence has always been plagued by a bit of an identity crisis. Because of this, and the fact that AI has become a popular hightech buzzword, it is often used inappropriately. But natural intelligences, and hence "real" AI systems, use concepts such as memory (of past actions), learning (reasoning about previous experience), and planning (establishing complex plans of action to achieve patterns of potentially conflicting goals). But the techniques discussed in this paper use none of these aspects of AI. They are merely incremental heuristics applied frame by frame with no memory, no planning, and no learning. Behavioral simulation superficially resembles artificial intelligence but is more closely related to artificial life [7, 3], the study of artificial systems with lifelike properties.
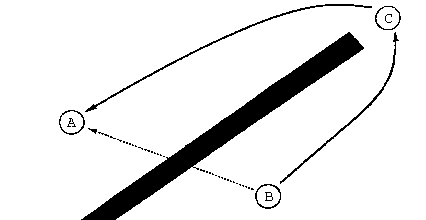
A typical goal for a moving object ("move from point A to point B") cannot always be reached by a simple-minded scheme that insists on heading toward B (see figure 1). Sometimes an intermediate goal ("C") must be identified and satisfied before the original goal can be met. These intermediate goals may well lie in exactly the opposite direction of a direct path to the original goal. For real-world problems, these goal/subgoal hierarchies can become very complex and require careful planning and good record keeping to accomplish. Systems capable of this sort of complex planning of potentially conflicting goals are described in the literature of the artificial intelligence field [4], but the obstacle avoidance techniques discussed in this paper do not rely on these sophisticated planning schemes.

Doing careful and detailed path planning requires global knowledge of the environment (positions and shapes of obstacles and goal locations in global space). To an independent actor that is exploring an unfamiliar environment, such global knowledge may not be available. If the exploring actor is allowed to learn from its experiences and to store them in its memory, however, it can eventually build a complete map of its environment. This internal map can then be used for global path planning. For example, a pair of birds will bumble around an unfamiliar territory looking for a good place to build their nest, but by the time they are shuttling back and forth to feed their chicks, their flight becomes quite nimble and the paths they select are well optimized.
In nature we note that animals seldom bump into things, but when stressed and in unfamiliar environments they do sometimes end up trapped in "dead ends." This could be seen as evidence of planning done on the fly, which is only valid for the short term and local environment. It is a sort of "optimistic planning": proceed in the most likely direction, skirting along any intervening obstacles, and hope that a path to the final goal becomes apparent some time in the future. Such a navigation technique works fine when the obstacles are sparsely distributed and are generally convex in shape. (See for example the structure of the environment used in Breaking the Ice [9] in Figure 2.) But "optimistic planning" is obviously a naive approach and cannot adequately deal with complicated maze-like environments in which individual obstacles are concave in shape or in which groups of obstacles abut together to form concave structures.
These techniques presume some ability to deal with the environment as a geometrical model. The world is defined in terms of points in three space and surfaces between them. For an object to move it must determine which obstacles e relevant to its path and determine which way to steer. In these descriptions use of the first person plural ("we", "our moving object") is intended to evoke the shift in perspective that is required to best understand local behavior from the moving object's own point of view.
The steer away from surface ("force field") approach supposes that a force field is emanating from the surface of the obstacle. The flying object is accelerated away from the surface of the obstacle by a force whose strength is inversely related to distance. Often the field can be represented by a single equation and so the steering acceleration can be easily calculated. But the motion produced by this technique does not correspond very well to our intuitive notion of steering around obstacles. If we are moving directly toward a wall we need to decide which way to turn to avoid a collision. But the force field from the wall will be directed exactly opposite to our velocity. As a result we will not be turned to either side but rather we will just decelerate to a stop.
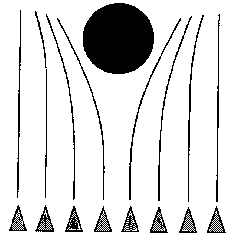
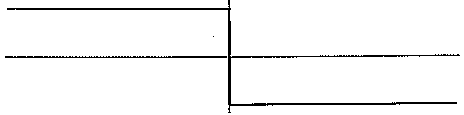
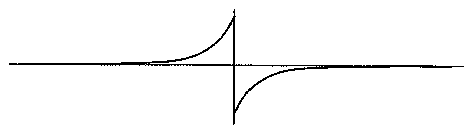
One way to picture this effect is the "lateral acceleration as a function of horizontal offset." An object is moving along on the X-Z plane, parallel to the Z axis, towards a cylinder centered on the Y axis (see figure 3). Consider the paths that result for various values of the X offset. Basically those paths that start to the left of the obstacle veer to the left and those on the right veer to the right. But the significant issue is the relation of the lateral acceleration to the horizontal offset. For the "steer away from surface" model this relationship has a "dead spot" in the middle (figure 4).
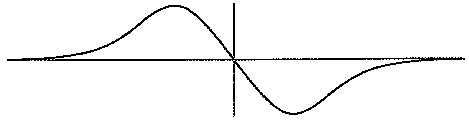
Another important property of an obstacle avoidance technique is directional discrimination. A moving object needs to react to the obstacles that block its path, but it must also ignore obstacles that are not along its path. The moving object needs to have a sort of "tunnel vision", generally ignoring obstacles that are off to the side or behind it. This is presumably why horses that work in crowded environments are fitted with blinders.
The "steer away from surface" obstacle avoidance technique has no directional discrimination at all. The global direction of the steering force is the same at a given global position regardless of the direction in which we are moving. So the same force that would tend to steer us away from an impending collision with an obstacle will also steer us away from a harmless attempt to fly alongside the obstacle. Ideally a moving object will be much more sensitive to obstacles directly in front of it than any others. Because sensitivity to the force field is uniform in all directions, the effect of the force field tends to be too strong when flying harmlessly alongside and too weak when flying directly into the obstacle from further away. Small steering accelerations applied earlier make for much more robust obstacle avoidance behavior.
The steer away from center technique basically considers the obstacle to be a point and says to steer in the direction opposite to that center point of the obstacle. If the center point is to the left of our path, we turn toward the right, if the center point is above our path, we dive down, and so on. The raw "steer away from center" technique is not very practical. It is similar to a spherical force field that is uniform over all distances. But it does have a better "lateral acceleration as a function of horizontal offset" response when we are flying directly into an obstacle. There is no "dead spot" near the center line of the obstacle (see figure 5).
It is possible to debug some of the shortcomings of this technique, although it is listed here primarily for completeness. For example there could be a distance limit, a maximum radius from the center point, hence the obstacle would be represented as a sphere. A moving object could simply ignore any obstacles further away than this radius. As with with the force field model, the steering behavior's strength can be made a function of distance. It would also be possible to sharpen the directional discrimination of this technique by making it active only when an obstacle is directly ahead of our moving object, as is discussed in more detail below.
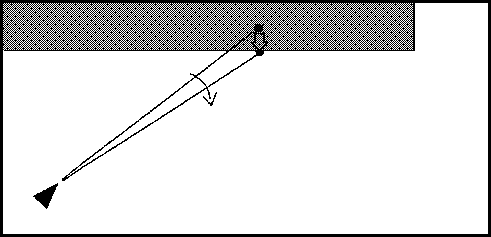
The steer along surface ("curb feeler") technique is familiar to anyone who has ever waLked down a darkened hallway, brushing a hand along the wall for guidance. The touch sensors on elevator doors and industrial robots, the whiskers on a cat, and the "curb feelers" on old automobiles are all based on the same concept. As long as nothing is within the range of the "curb feelers," all is well. But if a probe does touch an obstacle the possibility of a collision arises, and corrective action must be taken at once.
Physical probes of this sort are practical only for very short range detection and so for very low speeds. But a computational simulation of such a probe can be used to implement a simple and robust collision-avoidance technique. As previously noted, a moving object needs to be much more concerned with what lies directly ahead than with the rest of its environment. Imagine pushing a length of springy wire into a bin of bowling balls. The deflection of the wire by the surface of the balls allows the wire to find a clear path between the balls. Now consider a simulated "curb feeler" probe that extends directly forward from a moving object (along its local Z axis). When the probe touches an obstacle it will be deflected laterally. If the moving object then steers in the direction of the deflection the probe will swing away from the obstacle (see figure 6). This negative feedback will tend to keep the moving object from aiming at nearby obstacles, hence it will tend to steer away from collisions.
This avoidance technique is not very sophisticated, but a simple implementation can produce useful results because a certain amount of predictive behavior is obtained "for free." The length of the forward-pointing probe for the deflection calculation can be made proportional to the velocity vector of the moving object, times some constant of "predictiveness." So the forward tip of this probe represents the location where the moving object will be at some fixed time later if it does not change its course or speed. The predictiveness factor determines how much time prior to a potential collision is allocated to steering away from the obstacle.
Deflection of the probe tip can be achieved by using the same constraint system that would be invoked if our moving object were to bump into an obstacle. As the moving object approaches an obstacle, the probe tip will try to push into the obstacle, but the constraint maintenance system will push it back out. This restoration force can then be transferred back through the probe, applying a torque to the moving object and causing it to steer away from the potential collision.
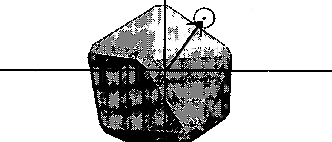
Steer towards silhouette edge: rather than consider surface orientation or centroid location, the heuristic here is to steer around an obstacle, head toward its nearest silhouette edge. Regardless of the shape compleity of an obstacle, its most significant feature is its silhouette from the point of view of the moving object. It can be thought of as a projection of the obstacle onto our moving object's local X-Y plane. A closed curve representing the silhouette can be directly computed from an obstacle's geometric shape database. This curve must actually be offset (enlarged) by an amount related to the size (maximum radius) of our moving object plus whatever "clearance" distance is desired between object and obstacle (see figure 7). If this offset silhouette curve surrounds the origin (of the moving object's local X-Y plane) then some portion of the obstacle is dead ahead on the current course. We must steer away to avoid a collision, and the most efficient direction to turn is toward that portion of the silhouette curve which is closest to the origin.
The following techniques get their information about the environment in the form of an image. The image represents "the view from the front window" of our moving object, a 2D map of some parameter of the environment sampled around the direction we are traveling. The image is processed and analyzed to determine which way to steer our moving object. Note that these techniques often need to adjust the bandwidth of the supplied images. Variable-resolution image formats (such as MIP maps [11]) are probably most appropriate.
Using the fuzzy silhouette:, a low-pass filtered silhouette image. Consider a image of a white painted obstacle, flatly lit, against a black field. The image is a map of places to avoid (in white) and places to go (in black). For our purposes it does not matter whether this image was made synthetically, using computer graphics techniques and a geometrical database, or by processing a real image from a real camera mounted in a real moving object.
The use of a geometrically defined silhouette was previously discussed. Analysis of the obstacle silhouette image could work the same way: a white pixel at the center of the image would indicate an obstacle straight ahead and so a potential collision. A spiral search pattern from the center of the image out could identify the first non-white pixel. We would then steer in the direction of this non-obstacle pixel.
But that transition from white to black pixels will more likely be a gray-scale ramp rather than a sharp cutoff. We could introduce an artificially sharp transition by thresholding the image, or we could deal graciously with the continuous nature of the image. That transition ramp along the obstacle's silhouette defines a gradient that can be used to find the nearest edge. The center of the image is analyzed looking for a gray-scale gradient. If for example there is a ramp from light gray on the left to dark gray on the right, then probably the bulk of the obstacle is on the left and the clear path is to the right. Hence the moving object would want to steer in the direction of the darkening gradient.
What about the case in which the center of the image is flat white and there is no measurable gradient? We could search outward looking far a silhouette gradient to follow, but it would probably be easier to expand the gradient. The easiest thing to do with an image is to remove the high spatial frequencies from it: to make it fuzzy. If there is no local gradient at the center of the map then maybe the image isn't fuzzy enough. Eventually the transition gradient from one silhouette edge will have expanded far enough to cross the center of the image.
Using the obstacle density image: steering based on a planar projection of the volumetric density of the obstacles ahead. If obstacles were constructed out of a translucent, jello-like substance we could imagine making maps of their density by some projection technique (making images by absorption of transmitted light, or x-rays, or whatever). In general these images would tend to show high density towards the center of the obstacle and would taper off to low density at the edges. These images could be analyzed similarly to the fuzzy silhouettes discussed above: filter the image until a strong gradient crosses the center of the image and steer from high density toward low density.
One advantage of dealing with obstacles as density fields is that it leads naturally into the notion of fractional obstacle-ness, which suggest a way to control complexity in the modeling of environments with lots and lots of individual obstacles. Consider an oak tree: inside we find obstacles and open space intertwined. But as we back away from the tree, at some point it becomes more useful to think of it not as either/or but rather as both obstacle and open space. Instead of many little obstacles and little open spaces, we want to treat it as a single larger entity having fractional obstacle-ness. An approach like this would allow efficient modeling of complex hierarchies of obstacles at an appropriate level of detail based on recursive subdivision.
A Z-buffer image provides a map of the distances to the nearest obstacles that lie along our flight path. This sort of image can be generated from the real world using various range-finding devices (radar, sonar, laser interferometer) or can be made synthetically from a geometric database. In fact a certain class of rendering algorithm produces a z-buffer image as a side effect of creating the visual image.
One way to use a z-buffer image would be to implement a version of the "steer along surface" technique discussed above. A more interesting one would be "steer towards longest clear path," searching around the z-buffer for maximum values, those which indicate that there is a long clear path to travel before an obstacle will be encountered. One approach would be to work with very low resolution images (say 3x3 or 5x5 pixels), exhaustively searching each datapoint and steering toward the pixel representing the longest clear path. This would probably work well in a simple environment, but if the field of view was crowded with many obstacles, by the time the image was filtered down to this handful of pixels the image would be too fuzzy to resolve the small clear spaces between obstacles.
A better approach would be to make a context-directed search of the image working from lowest resolution up to highest. For example a 2x2 image of the scene would be examined to determine that the upper right quadrant has the largest Z values. Then attention would be shifted to the upper right quadrant of a 4x4 image of the scene, and so on. This approach still is prone to drowning out a single large value surrounded by smaller ones due to the averaging that happens as the image is filtered down. An alternate ''filtering'' technique would be, for example, to reduce a 2x2 neighborhood by taking the maximu n rather than the average value of the four subsamples.
Using a z-buffer image to "steer towards the longest clear path" is a very robust technique, even in very complex environments. It requires a consistent amount of effort to make a decision about steering, regardless of the complexity of the environment. This sort of constant-time algorithm is very attractive for real-time applications, such as the control of real vehicles. The main drawback of this technique is that, without a more sophisticated ability to learn and plan, it has a tendency to drive into local concavities that may turn out to be dead ends.
Finally, while these lie outside the scope of this paper, some mention should be made of techniques that do depend on capabilities of artificial intelligence systems.
Techniques for robot path planning draws on elements of computational geometry and artificial intelligence. It seeks to address the complex planning problems that arise when dealing with maze-like environments and tight physical constraints on motion.
The field of image understanding lies at the intersection of image processing and artificial intelligence. Image understanding systems start by processing images to remove noise and irrelevant information and to enhance the relevant information, then they analyze the image with feature extraction techniques. These symbolic features are then given to an expert system that reasons about them, eventually drawing conclusions and deciding on a course of action. Today, these techniques are very complex, costly, and difficult to make reliable. But it seems likely that they will eventually be capable of outperforming the simple techniques described previously. After all, humans (and most animals) navigate around unfamiliar environments primarily by the use of "image understanding" techniques.
[1] Herald Abelson and Andrea diSessa, "Maneuvering a Three Dimensional Turtle"
in Turtle Geometry: The Computer as a Medium for Exploring Mathematics, The
MIT Press, Cambridge, Massachusetts, 1981, pp. 140-159.
[2] Gul Agha, Actors: A Model of Concurrent Computation in Distributed Systems,
The MIT Press, Cambridge, Massachusetts, 1986.
[3] Valentino Braitenberg, Vehicles: Experiments in Synthetic Psychology, The MIT
Press, Cambridge, Massachusetts, 1984.
[4] David Chapman, "Planning for Conjunctive Goals" in Artificial
Intelligence volume 32, nurnber 3, July 1987, pp. 333-378.
[5] Carl Hewitt and R. Atkinson, "Parallelism and Synchronization in
Actor Systems,"
ACM Symposium on Principles of Programming Languages 4, January 1977,
Los Angeles, California
[6] Chris Langton, editor, "Proceedings of the Artificial Life Workshop, Los Alamos
National Laboratory, September 21-25, 1987", in Volume 6 of the Santa Fe Institute
Studies in the Sciences of Complexity, Addison-Wesley, to be published September
1988.
[7] Chris Langton and Kevin Kelly, "Toward Artificial Life", Whole Earth Review,
Spring 1988.
[8] Craig Reynolds, "Flocks, Herds, and Schools: A Distributed Behavioral Model",
Proceedings of SIGGRAPH '87, in Computer Graphics volume 21, number 4, July
1987,pp 25-34.
[9] Symbolics Graphics Division and Whitney/Demos Productions (Larry
Malone,
Philippe Bergeron, Craig Reynolds, Michael Wahrman, et. al.) Stanley and Stela in
Breaking the Ice, presented at the SIGGRAPH '87 film show, July 1987.
[10] Jane Wilhelms, "Toward Automatic Motion Control," IEEE Computer Graphics
and Applications, V7 #4, April 1987, pp. 11-22.
[11] Lance Williams, "Pyramidal Parametrics", Proceedings of SIGGRAPH '83, in
Computer Graphics volume 17, number 3, July 1983, pp. 1-11.
Craig Reynolds has changed affiliations since this paper originally appeared, for updated information see his home page. The contact information at the time of the paper's original appearance was as follows:
Symbolics Graphics Division
1401 Westwood Boulevard
Los Angeles, California 90024
(Electronic mail: cwr@Symbolics.COM)