
Figure A: a polyhedron in flow, with and without adaptive resampling.
|
A technique is presented for adaptive resampling ("remeshing") of a polyhedral surface which is undergoing complex shape change. The goal is to maintain approximately uniform vertex density (by maintaining approximately uniform edge length) despite the application of non-linear flow deformations to the vertices. The resampling algorithm adds new polyhedral detail in sparse regions where the surface is expanding and removes excess detail in crowded regions where the surface is contracting. In animation, the adaptive resampling is performed once per frame along with various choreographed deformation operations which move the polyhedral vertices along the streamlines of the flow. Resampling is based solely on the object's static geometry and requires no knowledge or analysis of the flow system being used to deform it, which allows free use of arbitrary and ad hoc flow systems.
CR Categories and Subject Descriptors: 1.3.5 [Computer Graphics]: Computational Geometry and Object Modeling -- Curve, surface, solid, and object representations, 1.3.7 [Computer Graphics]: Three-Dimensional Graphics and Realism -- animation.
General terms: algorithms
Additional Keywords and Phrases: curved surface, adaptive, subdivision, resampling, mesh generation, incremental, deformation, nonlinear, flow, fluid, turbulence, chaos.
Computer animation is based on imparting motion to geometric models. Techniques such as linear transformation and interpolation are commonly used to produce computer animated motion. These techniques move the vertices of a polyhedron without altering the topology of its connecting structure of edges and faces. This is well suited for modeling a wide range of materials that are either rigid or elastic. Portraying other kinds of motion and material require different modeling techniques. This paper will discuss a new model suitable for fluid-like objects in flow-like motion.

The method described here makes polyhedra flexible and yielding enough so that they seem to be "fluid" when immersed in a suitable flow field. The resulting polyhedral models are suitable to animate flowing objects, to model objects shaped by flow, and to act as a "tracer" to help visualize flow patterns. Depending on the type of flow, observers often use terms like "putty", "clay", or "taffy" to describe the visual effect of applying flow transformations to surfaces. Figure A compares the naive approach of applying flow to a polyhedron's existing vertices to the result obtained with adaptive resampling. Other animated examples of this technique can be found in Ductile Flow [REYN90] and in the "flow sculptures" in Virtually Yours [ELSO91].
Most computer animation is choreographed with linear transformations or with simple deformation such as linear interpolation. These are useful and practical techniques that adequately describe many but not all motions. Some simple example of non-linear motions include: twists, tapers, bends, spirals, and vortices. More complex examples of non-linear motions from the real world include: a wisp of smoke curling up from a candle, cream being poured into coffee, the formation of marble, kneading bread dough, and pulling taffy.
Fluid motion, and particularly turbulent fluid motion, requires a very different kind of model for motion. In this paper it will be called flow animation. The basis of flow animation is a type of non-linear transformation that represents the flow. This flow transformation is an arbitrary mapping of points into points. (Usually they are points in XYZ space, also known as "R3".) In the application described here, a flow is typically represented as a program that computes this mapping. To animate a geometrical model, the flow transformation is mapped over the model's defining points, be they particles in a particle system, or vertices of a polyhedron, or control points of a higher-order surface.
This paper describes an adaptive polyhedral resampling technique that is suitable for use with flow animation. Flow animation itself is outside the scope of this paper. For a more detailed discussion, the interested reader should consult the following references for applications of flow animation to: particle systems [SIMS90], bird flocks [GIRA90], aerodynamics [WEJC9l], and image processing [SIMS92]. A relevant but less closely related model of fluid dynamics intended for animation is in [KASS90]. Flowing surfaces lofted between streamlines are used in [HELM9l] to help visualize the boundary surfaces between characteristic regions of turbulent fluid flow system, based on a topological analysis of the flow. This paper contains some very nice illustrations and good background information on turbulent fluid dynamics. An early catalog of flow-like deformations can be found in [BARR84]. Flow animation can also be driven by flow data measured in the real world or simulated with computational fluid dynamics.
Sampling theory and sampling techniques have a rich literature of their own, and adaptive sampling is a widely used concept applicable to a wide variety of problems. This section will provide some background on the applications of adaptive sampling and adaptive subdivision that are specific to computer graphics.
In [CATM74] adaptive subdivision was used to decompose bicubic patches to the pixel level for texture mapping and rendering. In [DIPP84] adaptive subdivision was used to partition scene complexity so as to balance the load on each of several parallel rendering processors. Adaptive subdivision is used in [SCHM86] as a type of data compression technique, attempting to approximate a high resolution array of measured altitude data by fitting a series of surface patches at various levels of detail. In [HERZ87] curved ("deformed") surfaces are adaptively subdivided into triangles for rendering such that visual artifacts are reduced without over-sampling. A similar approach is taken in [HALL90] for implicitly defined surfaces. Both [CAMP90] and [BAUM9l] discuss adaptive subdivision (adaptive "mesh generation") of polyhedral scenes in preparation for rendering by radiosity techniques. A technique for recovering polyhedral representations of shapes from voxel data is presented in [MILL9l] where polyhedral "balloons" are inflated inside a voxel data set and adaptive polyhedral subdivision is used to allow the surface to stretch as required.
A polyhedron is almost the antithesis of a curved surface, it is made up of straight edges and flat faces. Yet it is a time honored tradition in computer graphics to use polyhedrons to approximately represent curved surfaces. Rendering techniques such as Gouraud shading [GOUR7l] have long been used to portray polyhedral objects as if they were smoothly curved surfaces. When we look at a cube it is difficult to imagine any curvature, but as polyhedra become more mesh-like it becomes hard not to interpret them as curved surfaces. By "mesh-like polyhedra" we mean to suggest properties such as these: (1) the average edge length is much shorter than the average diameter of the whole polyhedron, and (2) the average dihedral angle between adjacent faces approaches 180 degrees.
A rough analogy can be drawn between the polyhedral representation of a curved surface and the discrete sampling of a continuous signal. (Discrete samples of a continuous signal taken at a certain rate will faithfully portray the signal up to a certain frequency. A polyhedral mesh of a given spatial frequency will faithfully represent (to a given tolerance) the surface up to a certain curvature.) If we sample the curved surface "frequently enough", the polyhedron whose vertices are those samples will be a "reasonable" representation of the surface. It is outside the scope of this paper to attempt to formally define those quoted terms, but most practitioners in the field have some intuitive understanding for appropriate average edge length. Once a suitable range of edge lengths is determined by the user, it will be maintained automatically by the adaptive polyhedral resampling technique as the surface is deformed.
During each animation frame, flow operations are applied to the vertices of a mesh-like polyhedron. This causes the vertices to move along the streamlines of the flow. The adaptive resampling operation is applied each frame to preserve the desired modeling quality. This operation takes two parameters: a maximum edge length threshold and a minimum edge length threshold. These two edge length threshold values bracket the distance between nearby vertices (samples). They are selected based on the nature of the flow system and the quality of modeling required. Values are chosen to balance modeling quality against computing time and memory requirements.
The maximum length threshold defines a (minimum) "shape sampling frequency" for the polyhedron. The curved streamlines of the flow space will be approximated by straight edges of (at most) this length. The adaptive resampling ensures that the polyhedron will be as flexible and yielding as necessary. It is always subdivided into small enough bits so that the nonlinear flow space can smoothly perturb its shape. As the flow alters the shape of the polyhedron some of the sample points will get stretched apart. When a polyhedron's edge becomes larger than the maximum length threshold, the edge is subdivided, along with its neighboring faces. Because this happens when the edge or face is still small and inconspicuous, polyhedral elements never become large enough to cause artifacts in the apparent curvature.
Conversely, the flow may compress portions of a polyhedron, pushing its vertices too close together. When a polyhedral edge became smaller than the minimum length threshold it is removed by "unsubdivision". Compression is is less likely to cause artifacts than expansion, but extra points are needless overhead and so are a source of inefficiency.
The net effect of this ongoing subdivision and "unsubdivision" is that the surface maintains an approximately constant sampling density or level of detail regardless of how the object is stretched or compressed by the flow. In Figure B we see a polyhedral mesh being deformed by a circular region of expansion in the upper right and an overlapping circular region of contraction in the lower left.
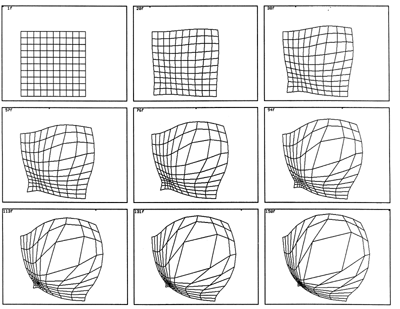
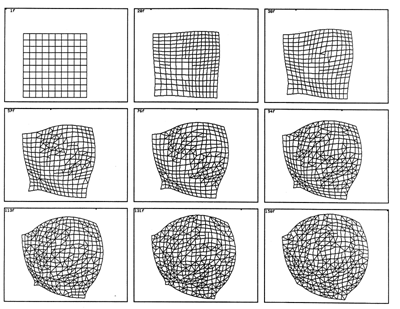
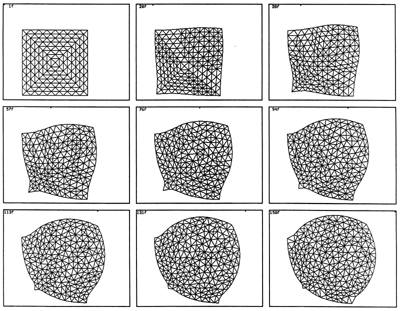
There is a tension between these opposing processes. The. flow causes portions of the surface to expand which become gist for the subdivider, and the flow causes other portions of the surface to contract which invokes the "unsubdivider". The difference between the maximum and minimum length thresholds defines a sort of hysteresis. As the upper and lower thresholds get closer there will a lot of "thrashing" (many sample points coming and going with little net change) but the result will be a very uniform sampling density. If the upper and lower thresholds are set further apart there will be a wider range of element sizes present, and much less adaptation will be required. A good compromise seems to be when the lower threshold is about 40% of the upper threshold. The lower threshold should be less than 50% of the upper threshold to avoid interference between the two opposing processes.
When the flow moves polyhedral vertices apart, the edges between them get longer, and the sampling density goes down. Subdividing the polyhedral elements solves these problems. New vertices are introduced which increases the sampling density and the long edges are split into shorter ones.
The first version of the subdivider used in this work was developed in mid 1990. This was the version used in the production of animation for [REYN90] and [ELSO91]. It dealt with arbitrary polyhedron and imposed no restrictions on polyhedral edge topology. However, it was observed that the adaptive resampling operation tended to produce polyhedra whose faces were predominately triangles. If it was guaranteed that all faces of the polyhedra were triangular, the subdivision algorithm could be simplified. (We will use the term deltahedron [STEW80] for these polyhedron with all triangular faces.) A version of the subdivider for deltahedra was implemented late in 1991. An arbitrary polyhedron can be converted into a deltahedron by a triangular decomposition its faces at animation initialization time. Both of these subdivision techniques seem to work well and both will be described here. Note that deltahedra have other desirable properties for modeling and rendering, for example their triangular faces are inherently planar and convex.
The original approach used for subdivision of arbitrary polyhedra was based on a plane cut operation supplied by S-Geometry [SGEO90], the underlying 3d geometric modeling system. This generic operation could be applied to whole polyhedra or their individual edges and faces. To subdivide a polyhedron the basic approach was to loop over all of its edges and then all of its faces, subdividing each element in turn. To subdivide a given element: its XYZ bounds are measured and the longest dimension was chosen, then the element is plane cut, perpendicular to the longest axis.
A simple approach is to always make a single cut, dividing the element in two. This works well as long as the polyhedron is already "well meshed" and is expanding gradually. Here and there elements will expand past the maximum length threshold and they will be cut in half. But if the expansion happens too rapidly it is possible that an element may be larger than twice the maximum length threshold, so cutting it in half would not be enough. We also want the subdivider to be able to handle the initial subdivision of arbitrary polyhedra on the first frame. For these reasons, the element subdivision needs to be a little more complicated, either by making multiple parallel cuts (like slicing bread) or by cutting once and then recursively subdividing the two parts. The initial implementation used the "bread slicer" approach:
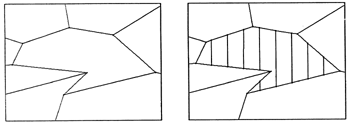 Figure C: (arbitrary polyhedron case) slicing a face
with a series of planes parallel to its longest axis.
Figure C: (arbitrary polyhedron case) slicing a face
with a series of planes parallel to its longest axis.
|
In the arbitrary polyhedron case, it is possible to have a large face made up of many short edges. In the deltahedron case however, so a large triangular face must contain a large edge. Hence for deltahedrons we can just loop over all of the edges, find the long ones, and cut them in half. As we do this, we also subdivide the two triangular faces that share the long face. This process repeats until no long edges remain:
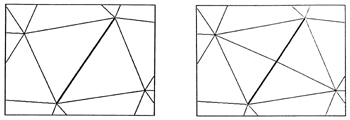 Figure D: (deltahedron case) splitting a long edge and its two
adjacent triangular faces.
Figure D: (deltahedron case) splitting a long edge and its two
adjacent triangular faces.
|
The techniques in [HERZ87] and [HALL90] also seek to subdivide curved surfaces, but they seek to concentrate samples along sharply curving portions of the surface. This is a valuable optimization when the deformations are static. But in the application described here, the flow is dynamic and the subdivider cannot "know" where samples should be concentrated, so a uniform subdivision is preferred. Both [CAMP90] and [BAUM9l] do subdivision much like that described here, the differences being that their criteria is not purely element size but has to do with equalizing illumination energy, and aligning cuts with shadow boundaries. [BAUM9l] has extra rules to deal with T-joints and faces with poor "aspect ratio". The "inflation" in [MILL9l] is identical in effect to the subdivider described here. The only difference is, as detailed in [MILL90], the localized subdivision is a l-to-4 split of triangular faces (instead of a l-to-2 split of edges) followed by an analogous splitting of neighboring faces.
When the flow moves polyhedral vertices together, the edges between them get shorter, and the sampling density goes up. "Unsubdividing" the short edges solves these problems. Some of the vertices are merged which decreases the sampling density and the short edges are removed.
To implement the "unsubdivision" portion of the adaptive polyhedral resampler, we need only loop over the edges of the polygon and somehow get rid of the edges that are too short. S-Geometry [SGEO90] provides an operation on its winged edge database called collapse. This operation replaces an edge and its two vertices with a single vertex. (See Figure E.) The effect is as if the edge had shrunk until its two endpoints merged into one.

It is possible to implement "unsubdivision" by finding and collapsing each face whose area is below a given threshold. In the implementation described here this approach was tried and later abandoned because the edge-based "unsubdivider" was less complicated and worked just as well.
While adaptive subdivision has been used by many researchers to address many types of problems (see section "Adaptive Subdivision"), there are very few references to anything like "unsubdivision" in the literature. When generating meshes for finite element analysis or radiosity, care must be taken to avoid short edges and malformed elements. The diagram in Figure 6 of [BAUM9l] could be interpreted as an illustration of the sort of "unsubdivision" discussed here, but in fact that picture actually shows two alternative meshing strategies, rather than a before and after comparison. Similarly, while it is not a method to get rid of existing short edges, [HALL90] discusses a heuristic applied during adaptive subdivision intended to prevent the formation of short edges (specifically faces with bad "aspect ratios").
As described so far, the adaptive polyhedral resampler will work well on surfaces that are characterized by smooth gentle curves. Because the "unsubdivision" phase removes edges shorter than a certain length it tends to act as a low pass filter on the shape. Polyhedral details with high spatial frequency will tend to be lost to "unsubdivision". While generally this is the desired result, it turns out that certain high frequency features are important and need to be retained.
Consider a cube being animated through a simple flow. While the cube will quickly become curved as it follows the streamlines, we would like it to retain its characteristic sharp edges and pointed corners. (See, for example, Figure A.) The adaptive resampler (as so far described) will tend to smooth out the shape of the "cube" due to the low pass filtering effect. After many iterations (frames of animation) it would be hard to tell the difference between a mesh that had started out shaped like a cube from one that had started out shaped like a sphere.
Somehow we would like to alter the action of the "unsubdivider" in the vicinity of certain characteristic edges or feature lines of the mesh so that it avoids distorting the characteristic shape. One approach that might work would be to manually designate certain edges of the original polyhedron as special, and to have the "unsubdivider" preserve those marked edges.
However there is another class of feature that needs special treatment. A flow system can cause a surface to be stretched into long thin tendrils. (Imagine honey being poured from a jar.) If the tendril's diameter is less than the minimum edge length threshold of the resampler, then the edges that make up the tendril will all be collapsed, causing the tendril to wither away. In this case it would not be practical to manually mark the edges of the tendril for preservation, since those edges are probably created on the fly during the flow animation.
Fortunately, a single technique can handle both of these cases. We will add another parameter, an angle threshold, to the adaptive polyhedral resampler. By measuring the dihedral angle formed by an edge's two adjacent faces, we can classify each edge as hard or soft relative to the the angle threshold parameter. The hard edges are the ones we want to preserve. The reason this also handles the tendril case is that as the tendril gets thinner, its structure will be like a tube with fewer and fewer faces around its circumference. Eventually the tendril will be a tube with a triangular cross section, edges parallel to the tube will be classified as hard and they will be preserved.
As described above, when an edge is collapsed it leaves behind one vertex. Normally, that vertex will be at the same position as the midpoint of the collapsed edge. To preserve hard edges we make the following modification. Before the collapse we count the number of hard edges that meet at each of the two vertices. The vertex with the most hard edges "wins" and it becomes the location of the new vertex. The result of this is that while the mesh topology may change near the hard edge, but the geometry stays about the same.
An adaptive resampling technique has been presented which allows polyhedral surfaces to be animated through the use of choreographed flow. These techniques have been used in the production of two animated films. One of the flow systems used in [REYN90] is the Lorenz strange attractor. That these algorithms work well even in the face of chaotic flow provides evidence that they are dependable and robust.
Representing a curved surface with a polyhedron is an approximation. The adaptive resampling algorithm operates on that flawed polyhedral model during flow animation and so the surfaces it produces differs from the "exact solution". The sources of error are that: (1) cutting a polyhedral edge represents a linear approximation to (a chord of) the curved surface, and (2) collapsing an edge potentially moves vertices from the curved surface to the midpoint of the edge. In most cases these errors will be negligible. However turbulent or chaotic flows have the property that very small features be magnified enormously.

The adaptive resampling works by adding and removing polyhedral detail. As a result the surfaces are somewhat unstable. There is some amount of "sizzle" temporal noise as the polyhedral edges come and go. This can lead to visual artifacts in rendered animation, particularly in regions where specular reflection magnifies surface irregularities. Since these irregularities flow along with the surface they are not very disturbing.
The current implementation's three threshold parameters are specified as constants. Instead, active functions could be used to compute threshold values on the fly. This would allow, for example, the sampling density to be dependent on the perspective of the camera. Objects close to the camera would use finer meshes and objects far away would use coarser meshes. This approach may have some utility even when flow animation is not being used.
A specific goal in both [BAUM9l] and [HALL90] is to avoid creating faces with "bad aspect ratio" (that is, long and skinny faces). This implementation usually avoids such faces, but takes no specific action to prevent them. Perhaps it could be extended to do so.
It would be interesting to apply a similar adaptive resampling technique to higher order surface patches. The modeling error and noise problems mentioned above would probably be much reduced if curved surface patches were used. One approach would be to use the deltahedral algorithm as described above and then to fit a triangular patch [BARN74], [BOEH85], [LOOP90], [SEDE84] to each of the polyhedral faces.
The work described here was supported by the Graphics Division of Symbolics Inc. The current implementation of the adaptive resampling algorithm was implemented in Symbolics Common Lisp and New Flavors, using facilities provided by Symbolics' S-Geometry 3d modeling system and S-Dynamics animation scripting system. Special thanks go to Larry Malone, the author of S-Geometry for endless patient help during the design of this software and the production of animation for Ductile Flow and Virtually Yours. Thanks to Matt Elson for showcasing this work in Virtually Yours. Thanks for help and support also go to: Lisa Berson Reynolds, Andy Kopra, Tom McMahon, Kevin Hunter, Jim Ryan, Ralph Seibert, Anoosh Mostowfipour, Bart Gawboy, Allan Wechsler, John Aspinall, Brian Barsky, and David Breen.
[BARN74] Robert Barnhill, "Smooth Interpolation Over Triangles", Computer Aided Geometric Design (Barnhill and Riesenfeld editors), Academic Press, 1974, pages 45-70
[BARR84] Alan H. Barr, "Global and Local Deformations of Solid Primitives", Computer Graphics (Proceedings of SIGGRAPH '84), Volume 18, Number 3, July 1984, pages 21-30.
[BAUM9l] Daniel R. Baum, Stephen Mann, Kevin P. Smith, and James Winget, "Making Radiosity Usable: Automatic Preprocessing and Meshing Techniques for the Generation of Accurate Radiosity Solutions", Computer Graphics (Proceedings of SIGGRAPH '91), Volume 25, Number 4, August 1991, pages 51-60.
[BOEH85] Wolfgang Boehm, "Triangular Spline Algorithms", Computer Aided Geometric Design, Volume 2, Number 1-3, September 1985, pages 61-67.
[CAMP90] A. T. Campbell, III and Donald S. Fussell, "Adaptive Mesh Generation for Global Diffuse Illumination", Computer Graphics (Proceedings of SIGGRAPH '90), Volume 24, Number 4, August 1990, pages 155-164.
[CATM74] Edwin Catmull, "A Subdivision Algorithm for Computer Display of Curved Surfaces", University of Utah, Computer Science Department, UTEC-CSc-74-133, December 1974.
[DIPP84] Mark Dippe and John Swensen, "An Adaptive Subdivision Algorithm and Parallel Architecture for Realistic Image Synthesis", Computer Graphics (Proceedings of SIGGRAPH '84), Volume 18, Number 3, July 1984, pages 149-158.
[ELSO9l] Matt Elson (director) et al., "Virtually Yours", SIGGRAPH '91 Electronic Theater, to appear in SIGGRAPH Video Review.
[GIRA90] Michael Girard and Susan Amkraut, "Eurhythmy: Concept and Process", The Journal of Visualization and Computer Animation, Volume 1, Number 1, August 1990, pages 15-17.
[GOUR7l] H. Gouraud, "Continuous Shading of Curved Surfaces", IEEE Transactions on Computers, C-20(6), June 1971, pages 623-628.
[HALL90] Mark Hall and Joe Warren, "Adaptive Polygonization of Implicitly Defined Surfaces", IEEE Computer Graphics and Applications, Volume 10, Number 6, November 1990, pages 33-42.
[HELM9l] James L. Helman and Lambertus Hesselink, "Visualizing Vector Field Topology in Fluid Flows", IEEE Computer Graphics and Applications, Volume 11, Number 3, May 1991, pages 36-46.
[HERZ87] Brian Von Herzen and Alan H. Barr, "Accurate Triangulations of Deformed Intersecting Surfaces", Computer Graphics (Proceedings of SIGGRAPH '87), Volume 21, Number 4, July 1987, pages 103-110.
[KASS90] Michael Kass and Gavin Miller, "Rapid, Stable Fluid Dynamics for Computer Graphics", Computer Graphics (Proceedings of SIGGRAPH '90), Volume 24, Number 4, August 1990, pages 49-57.
[LOOP90] Charles Loop and Tony DeRose, "Generalized B-spline Surfaces of Arbitrary Topology", Computer Graphics (Proceedings of SIGGRAPH '90), Volume 24, Number 4, August 1990, pages 347-356.
[MILL90] James V. Miller, On GDM's: Geometrically Deformed Models for the Extraction of Closed Shapes from Volume Data, Master's thesis, Rensselaer Polytechnic Institute, December 1990.
[MILL9l] James V. Miller, David E. Breen, William E. Larsen, Robert M. O'Bara, and Michael J. Wozny, "Geometrically Deformed Models: A Method for Extracting Closed Geometric Models from Volume Data", Computer Graphics (Proceedings of SIGGRAPH '91), Volume 25, Number 4, August 1991, pages 217-226.
[REYN90] Craig Reynolds, "Ductile Flow", SIGGRAPH '90 Electronic Theater, to appear in SIGGRAPH Video Review.
[SCHM86] Francis J. M. Schmitt, Brian A. Barsky, and Wen-Hui Du, "An Adaptive Subdivision Method for Surface-Fitting from Sampled Data", Computer Graphics (Proceedings of SIGGRAPH '86), Volume 20, Number 4, August 1986, pages 179-188.
[SEDE84] Thomas W. Sederberg and David C. Anderson, "Ray Tracing of Steiner Patches", Computer Graphics (Proceedings of SIGGRAPH '84), Volume 18, Number 3, July 1984, pages 159-164.
[SIMS90] Karl Sims, "Particle Animation and Rendering Using Data Parallel Computation", Computer Graphics (Proceedings of SIGGRAPH '90), Volume 24, Number 4, August 1990, pages 405-413.
[SIMS92] Karl Sims, "Choreographed Image Flow", to appear in the Journal of Visualization and Computer Graphics, 1992
[STEW80] Bonnie Stewart, Adventures Among the Toroids, second edition, 1980, published by the author: B. M. Stewart, 4494 Wausau Road, Okemos, MI 48864, pages 25-28.
[SGEO90] S-Geometry User Reference Manual, Symbolics, Inc, August 1990.
[WEJC91] Jakub Wejchert and David Haumann, "Animation Aerodynamics", Computer Graphics (Proceedings of SIGGRAPH '91), Volume 25, Number 4, August 1991, pages 19-22.
(4620 words.)
(submitted 1-7-92, "second printing" 1-10-92)